Vergleich zwischen verschiedenen Viskositätsmodellen
Viskositätsmessungen werden mit einem Hochdruck-Kapillarrheometer bei diskreten Scherraten durchgeführt. In Übergangszonen des realen Prozesses oder insbesondere in der Strömungssimulation ist für die Berechnung von Punkten zwischen den gemessenen Daten eine mathematische Funktion der Steigung der Viskosität als eine Funktion der Schergeschwindigkeit erforderlich. Daher wurden Modelle entwickelt, um den mathematischen Zusammenhang der gemessenen Viskositätsdaten als eine Funktion der Scherrate zu beschreiben.
Die Modelle haben unterschiedliche Stärken und Schwächen und oftmals ist das jeweilige Modell nur für bestimmte Materialien geeignet. Die folgende Auflistung der Modelle beschränkt sich auf die rheologischen Modelle, die in der GÖTTFERT Standard Software für die Kapillarrheometer integriert sind.
Allgemeine Beschreibung verschiedener Bereiche der Funktion von Viskosität gegen Scherrate
Die prinzipielle Steigung der Viskosität gegen Scherraten ist in der folgenden Abbildung dargestellt.
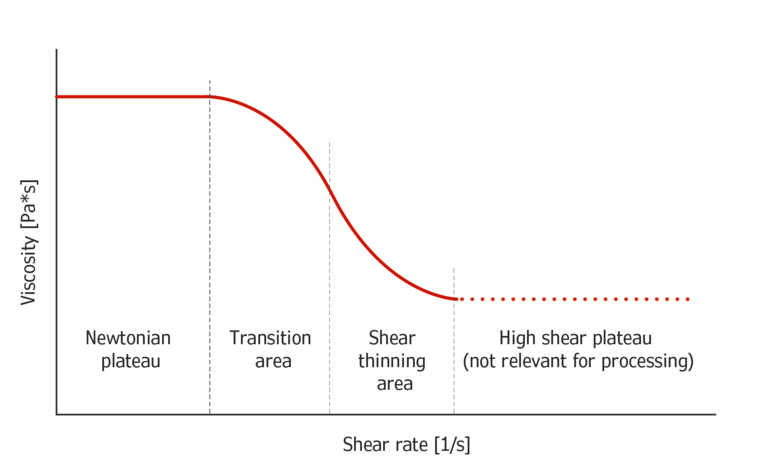Abbildung 1: prinzipielle Steigung der Viskosität
Die Viskosität beginnt bei einem Niveau konstanter Viskosität, dem so genannten Newtonschen Plateau, und wendet sich dann in einem Übergangsbereich mit sich ändernder Neigung zum Scherverdünnungsbereich. Bei sehr hohen Schergeschwindigkeiten tritt entweder ein Schmelzbruch oder wiederholt ein Plateau auf, dieser Bereich ist jedoch für die Verarbeitung nicht relevant und nicht in üblichen Strömungsmodellen beschrieben.
Ostwald – de Waele (power law)
Vor allem Elastomere lassen sich mit diesem einfachen Modell, das die Steigung der strukturviskosen Fläche beschreibt, recht gut beschreiben.
Für thermoplastische Materialien ist das Ostawald – de Waele Modell weniger geeignet, da hier neben dem strukturviskosen Bereich auch die Übergangszone bis zum Newtonschen Plateau berücksichtigt wird. Es sollte nur im pseudoplastischen Bereich (Scherverdünnung) verwendet werden, da die Krümmung der Viskosität im Übergangsbereich nicht beschrieben wird.
Wenn es mit doppelter logarithmischer Achse gezeichnet wird, ist das Modell eine gerade Linie.
Carreau – Winter
Der 3-Parameter-Ausdruck umfasst auch den sogenannten Newton-Plateau-Bereich, Übergangsund Scherverdünnungsbereich. Das viskose Fließverhalten wird über einen weiten Scherratenbereich, insbesondere im Bereich größerer Scherraten, physikalisch sinnvoll beschrieben.
Die Null-Scherviskosität (Newton-Plateau) ist proportional zur mittleren Molmasse. Der Bereich der Molekulargewichtsverteilung hat Einfluss auf die Übergangszeit sowie auf den Viskositätsexponenten (Scherverdünnungsfläche).
Yasuda (modified Carreau – Model)
Yasuda ist ein erweitertes Carreau-Modell, das die Viskosität von verzweigten thermoplastischen Materialien beschreibt. Diese Art von Materialien zeigen eine typische Krümmung der Viskosität im Übergangsbereich zwischen Null-Scherviskosität und pseudoplastischem (Scherverdünnung) Bereich, die mit dem zusätzlichen Exponenten beschrieben werden kann. Typischerweise passt dieses Modell auch sehr gut bei niedrigen und auch hohen Scherraten. Wenn das Modell gut über die gesamte gemessene Scherrate passt, ist auch eine Extrapolation mit hoher Zuverlässigkeit möglich.
Muenstedt
Dieser 4-Grad-Polynom-Ausdruck ist eine mathematische Näherung der Viskositätsfunktion. Die Funktion stimmt in der Regel sehr gut mit den experimentellen Daten überein, aber aufgrund ihrer rein mathematischen Natur wird eine Datenextrapolation nicht empfohlen.
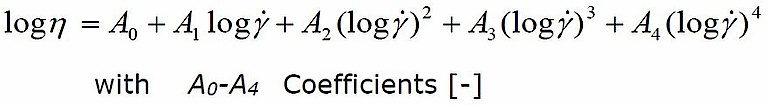
Cross
Das Cross-Modell ist dem Carreau-Winter-Modell sehr ähnlich. Jedoch wird der Exponent unterschiedlich angewendet, was zu einer etwas anderen Form der Kurve führt.
Vergleich von Modellen mit HDPE
Abbildung 2 zeigt das Ostwald-Modell, das aus Messdaten mit HDPE mit logarithmischer Skalierung berechnet wurde. Die Grafik zeigt, warum die Verwendung des Ostwald-Modells über den gesamten Schergeschwindigkeitsbereich dieses thermoplastischen HDPE-Tests wenig sinnvoll ist. Die typische Krümmung zu Beginn des scherentzähenden Bereichs kann nicht genau modelliert werden.
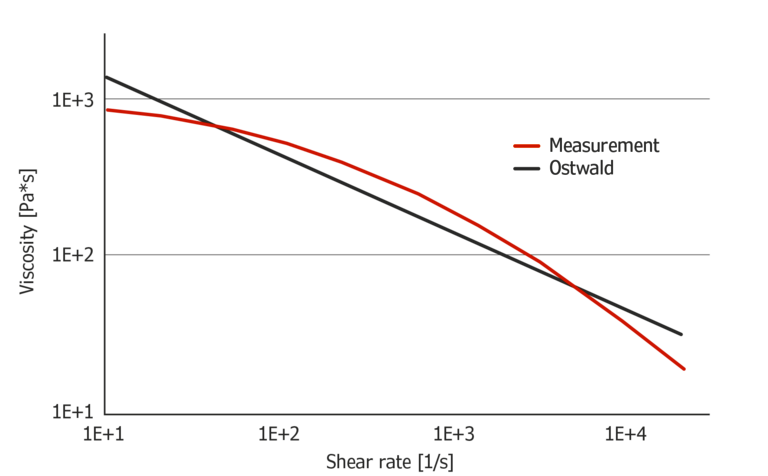Abbildung 2: Ostwald-Modell berechnet aus Messdaten von HDPE
Das in Abbildung 3 gezeigte Carreau-Modell passt zu den Daten genauer. Jedoch sind noch immer kleinere Unterschiede zwischen den gemessenen Daten und dem Modell zu erkennen. Das Cross-Modell passt mit den gemessenen Daten sehr gut. Es sind lediglich kleinere Abweichungen bei größeren Scherraten zu erkennen.
Im direkten Vergleich ist das Cross-Modell bei niedrigen Schergeschwindigkeiten genauer, während das Carreau-Modell für hohe Scherraten genauer ist. Die Krümmung der Modelle ist aufgrund der unterschiedlichen Position des Exponenten im Nenner der Gleichungen leicht unterschiedlich.
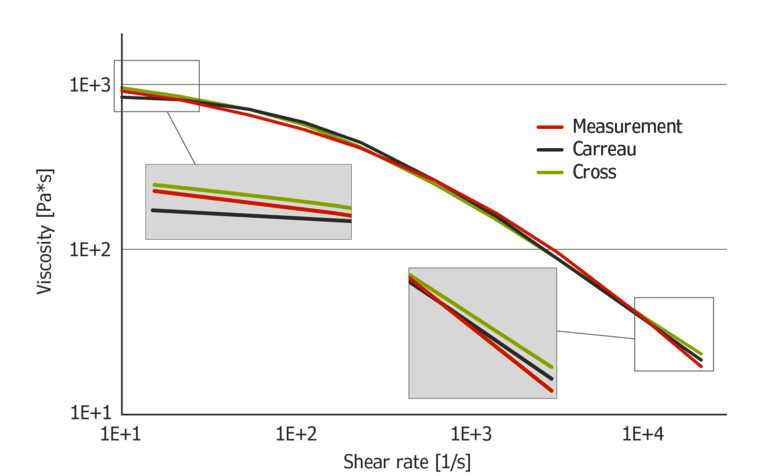Abbildung 3: Carreau und Cross-Modell berechnet aus Messdaten von HDPE
Abbildung 4 zeigt das Muenstedt- und Yasuda-Modell, das aus Messdaten mit HDPE berechnet wurde. Beide Modelle passen perfekt zu den Daten. Während die Muenstedt Formel eine rein mathematische Approximation der Daten darstellt, ist Yasudas Gleichung physikalisch plausibel.
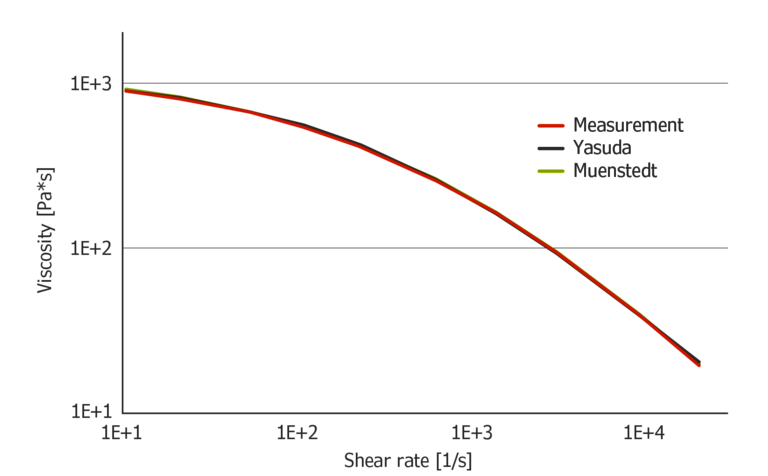Abbildung 4: Muenstedt and Yasuda Modell berechnet aus Messdaten von HDPE
Extrapolation der Daten
Abbildung 5 zeigt die Extrapolation von Daten mit den Modellen Carreau und Cross. Die Ergebnisse mit Carreau scheinen bei hohen Scherraten etwas plausibler zu sein. Bei niedrigen Schergeschwindigkeiten scheinen die Ergebnisse des Cross-Modells genauer zu sein.
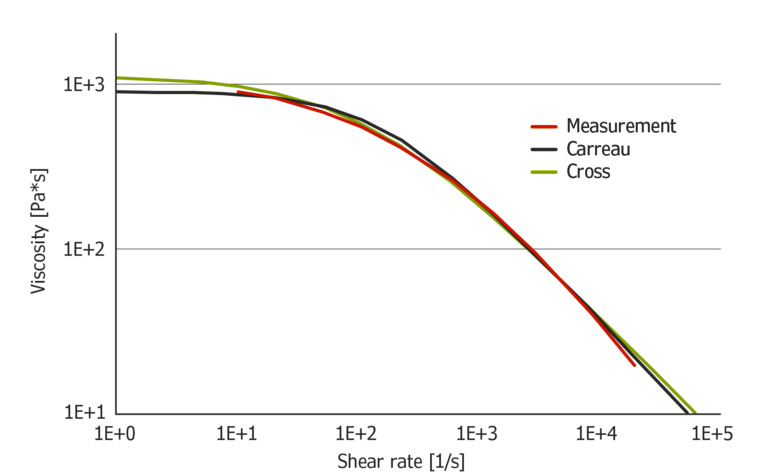Abbildung 5: Extrapolation von HDPE-Messdaten mit Carreau und Cross
Verglichen mit Cross und Carreau passen Muenstedt und Yasuda besser zu den Daten und sind daher besser für die Datenextrapolation geeignet, zumindest mit diesem Material.
Im Vergleich zu Muenstedt berechnet Yasuda geringfügig niedrigere Viskositäten bei niedrigen Schergeschwindigkeiten und etwas Höhere bei hohen Scherraten. Für die Extrapolation scheint Yasuda aufgrund seiner genauen Datenreplikation und physikalisch plausiblen Gleichung das am besten geeignete Modell zu sein.
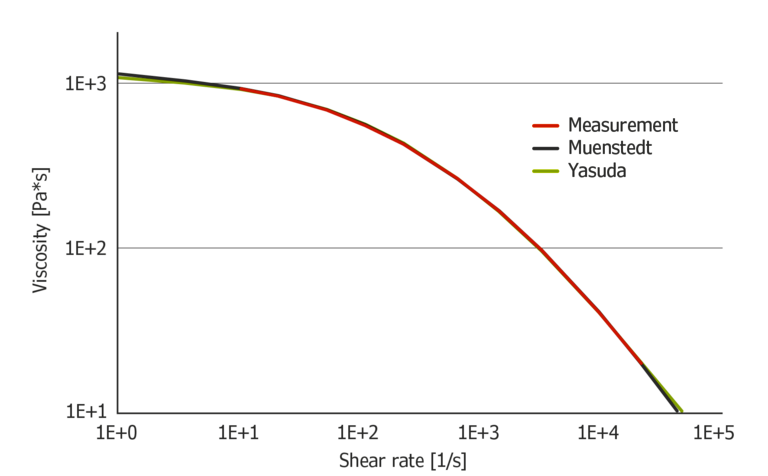Abbildung 6: Extrapolation von HDPE Messdaten mit Muenstedt and Yasuda
Das verwendende Modell ist immer abhängig vom verwendeten Material. Die Ergebnisse verschiedener Modelle sollten verglichen werden und das am besten geeignete Modell sollte für eine bestimmte Anwendung ausgewählt werden.
Der einfachste Weg, das beste Modell auszuwählen, ist der Vergleich des Korrelationskoeffizienten, der auch mit den Modellkoeffizienten gegeben ist. Die ideale Anpassung ist durch einen Korrelationskoeffizienten von 1 gegeben.
